Predictor Model of Root Caries in Older Adults: Reporting of Evidence to the Translational Evidence Mechanism
Abstract
Compared to younger adults, older adults are at greater risk for root caries. A model of root caries may assist dentists in predicting disease outcomes. OBJECTIVES: Using the Iowa 65+ Oral Health Survey, analysis was done to model the patterns of the root caries development in older adults.
Results:
The model effectively predicts root caries using an 18-month predictive cycle and is validated up to 36 months (two cycles), with no significant differences (Chi-square test p-values >0.1) between predicted and observed distributions. However, we do not have observed data for validation beyond 36 months since the model was designed to perform only at single or multiple 18-month cycles. As expected, the predicted distribution at 54-month (3 cycles) and the observed distribution at 60-month differed significantly (p<0.0001).
Conclusions:
The model demonstrated a high probability that a sound surface will remain caries free. However, one and multiple-surface lesions aggressively infect adjoining surfaces. Maturing of the carious lesion occurs with the 4-surface lesion, decreasing the probability of tooth loss. Thus, maintaining a sound root surface and early treatment intervention reduces the risk of tooth dysfunction (morphological destruction) and loss.
DATABASE FILTERS:
P: Tooth/Subject characteristics-Older adults, 65 years of age or more, male and female participants, regional rural Iowa residents, race unspecified, functional status-non-institutionalized level unspecified, risk level unspecified
I: Root caries
P (C-not applicable): Probability/Statistical significance for decision data only/Clinical significance-dataset over 20 years old/Utility data not included/Cost data not included/Meaning in practice undetermined.
O: Each year through a three year cycle, caries progression from a sound root surface
A: Data attached:
■ Published manuscript
□ Unpublished manuscript
□ Raw data
R: Primary author contact information present
INTRODUCTION
Root caries is an infectious disease process that originates on the root surface of a tooth but may extend to involve the enamel surface at the cervical region, other adjacent root surfaces, or both. Teeth become at risk for root caries when gingival recession is evidenced. Gingival recession is greatest in older adults, 90% of older adults demonstrating gingival recession of greater than or equal to 1 mm at 40% of sites affected with mean levels of over 2 mm [1].
The risk of root caries increases with age, particularly in older adults who are irregular users of dental services [2]. In describing the progression of untreated caries, the model of root caries [3] (Fig. 1) provides clinicians with a natural history (algorithm) of the disease process, its sequelae, and intervention points to limit or prevent tooth loss. This algorithm of root lesion progression begins with an exposed but caries free sound root surface. Demineralization of the root surface leads to the initiation of the root caries lesion, producing the incipient lesion. Once patent, the incipient lesion becomes a one-surface lesion. This one-surface lesion may lead to a multiple-surface lesion, involving two, three, or all root surfaces of the tooth.
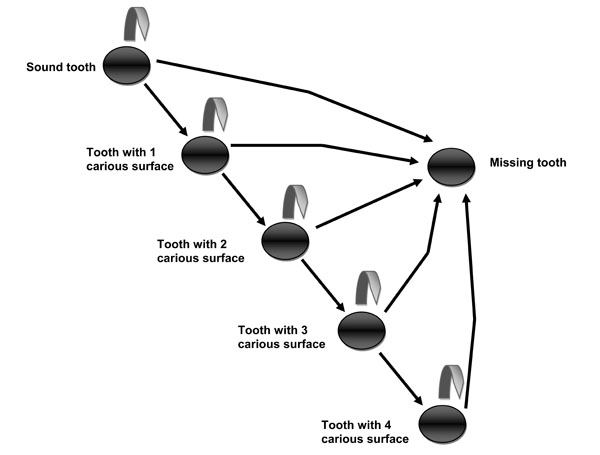
The natural history of root caries is an algorithm, visually representing root caries progression. At any time in the progression, a tooth may be loss, or be missing. The algorithm starts with a sound, caries free root surface. The sound tooth may remain caries free or progress to develop a one-surface lesion. Once patent, the one-surface lesion may lead to a multiple-surface lesion.
During normal aging, physiologic dentinal sclerosis occurs, decreasing the permeability of the dentinal tubules to bacterial progression. Among other factors, healing and the slowing down of the destructive carious lesion may result from a remineralization process. This remineralization process is promoted by salivary agents and agents delivered to the oral cavity with the use of professional therapies or personal, preventive oral hygiene routines [4]. As a result, a sound root surface may remain caries free, one or multiple-surface lesions may remain in their respective states, and each may not progress to infect other root surfaces of the tooth.
Dental sclerosis may favor spreading of a root surface lesion to adjoining surfaces of the tooth rather than cavitate the infected surface. In a 4-surface lesion, this pattern of morphological loss produces a characteristic collaring of caries extending circumferentially along the cementoenamel junction, below the clinical enamel crown of the tooth. The 4-surface lesion may become chronic. Loss of the root structure may be so significant that it undermines the support of the clinical crown. When tooth structure is compromised, the tooth is at a high risk for fracture, compromising oral or tooth function. The tooth may then be lost due to clinical outcomes that disallow its rehabilitation.
Using the algorithm, caries progression occurs as a random like behavior, evolving over time. Models that study these random, or stochastic, processes use probabilities. A Markov chain model is a commonly used model for a stochastic process [5]. In this paper, we will use the simplest Markov chain in which there are a finite number of states and a finite number of equidistant time points at which observations are made. Under this model, any tooth changes from one state to another state randomly with a determined probability in any given time interval. These probabilities are called transition probabilities and are the same for all time intervals.
The purpose of this study is to evaluate the incidence of root caries in older adults and model the changes of distributions of surfaces affected using a Markov chain model.
METHOD
Sample
Data from the Iowa 65+ Oral Health Survey [6], which provided longitudinal data on root caries over a period of 60 months in non-institutionalized adults, 65 years of age and older was used for model development. Baseline, 18, 36, and 60 month follow-up data were included for the analysis. Reversals of the caries diagnosis and scoring inconsistencies for each of the time points (18 and 36 months) were analyzed and previously reported [3].
Tooth status was diagnosed as sound or carious, identifying the specific surface affected with primary caries, and missing. The criterion for root caries was a discrete, well-defined, and discolored cavitation on the root surface in which the explorer entered easily and displayed some resistance to withdrawal. Any lesion in the enamel half of which extended apical to the cementoenamel junction was assumed to have originated on the root surface. If the lesion extended more than one-third of the way across the adjacent surface, it was considered a multiple surface lesion.
Data Set for Present Study
The tooth sample consisted of untreated, unrestored root surfaces. The original data set had 819 subjects and 26,208 teeth, with nominal 32 teeth for each subject. In our analysis, we consider each tooth as a sample. Among all the 26,208 teeth, only 9,344 have complete status information at all 4 time points. Missing values may be due to subjects lost to follow-up or added after baseline. For purposes of this study, assumptions were made: Missing values are missing at random (MAR), tooth status can only change to its same state or a worse state, and the probability distribution of incorrect diagnosis of tooth status is identical for all teeth and at all time points. Thus, teeth with missing values or reversals were excluded. As a result, data for 8,126 teeth was available for the final analysis (Fig. 2).
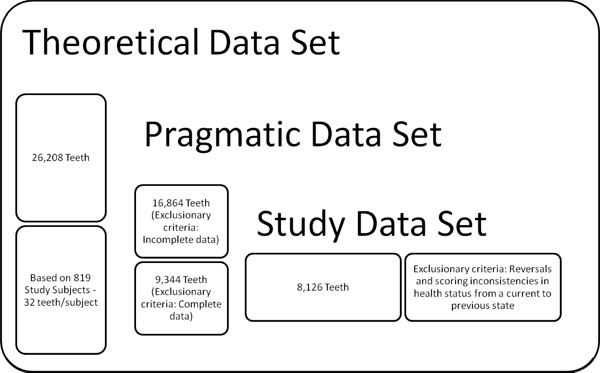
Study data set determination – Display of exclusionary criteria and number of teeth eliminated for analysis. Remainder is number of teeth subjected to Markov chain process.
The status of each tooth location may change over time, and at any time, including baseline, a tooth could be missing. For each time point, the status of these 8,126 tooth locations could be evaluated throughout the 60 month period.
The sample size for each time point was 8,126 tooth locations. Caries progression was observed either in the same state as the previous assessment or a degraded state, caries involving an adjacent surface. The analysis included only tooth locations with complete data at all 4 time points and having no reversals.
Analyses
For this study, there are three research questions. Firstly, what are the frequencies of a sound, one-surface, or multiple-surface root caries lesion assessed at various time points? Secondly, what is the probability that a sound, one-surface lesion, or multiple-surface lesion will remain in that state or progress to a more degraded state when assessed in a subsequent time point? Lastly, can the dynamics using a Markov chain model predict the distribution of the root caries lesion at a subsequent time given the distribution at the present time?
Markov Chain Model
The study evaluated the effectiveness of a Markov chain model using transition probability matrices for predicting the distribution of root caries and surface(s) affected. A Markov chain model [7] is a statistical model to describe a process, such as the development of root caries. In such a model, an observation or outcome in a specific time point is dependent only on its status in the immediately preceding time point. Longitudinal data in this study are used to determine the probability that a root surface either intact or with caries involving a specific surface or combination of surfaces, in one time point will remain the same or progress to further caries involvement in the next time point. The resultant probabilities are used to create a transition probability matrix. This matrix requires observations to be made at a minimum of two points, an initial and follow-up time point. A root surface that is sound [8] can remain sound or progress to develop caries. For example, a root surface that has a one-surface lesion can remain as a root surface with a one-surface lesion (1) or progress to develop a 2-surface [2], 3-surface [3], or 4-surface lesion [4], or be missing [9]. Being missing, or the final, terminating outcome of the progression of root caries is termed the “absorptive state”. The transition probability matrix forms the basis of the Markov chain model to study the dynamics of the manner and patterns through which a tooth develops root caries and advances toward further destruction.
Likelihood Ratio Test
The Likelihood Ratio Test (LRT) was used to test the stationary assumption for our Markov chain model, which asserts that the root caries progression from baseline to 18 months and from 18 to 36 months share the same transition probability matrix. The likelihood is a measure of how likely a hypothesis is true. The LRT is based on the ratio of two likelihoods: the first is determined by maximizing the likelihood function when the stationary assumption holds, and the second is determined similarly when this assumption is removed. The test statistic has an asymptotic Chi-square distribution. The LRT will assert whether the transition probabilities are operating as a stationary Markov chain, which allows us to use the same transition probability matrix for baseline to 18 months and from 18 months to 36 months.
Maximum Likelihood Estimate
Under the stationary assumption, the likelihood function is a measure of how likely a certain matrix is the true transition probability matrix given the data. The Maximum Likelihood Estimate (MLE) maximizes the likelihood function among all possible values of transition probability matrices. In other words, the MLE for the transition probability matrix is the most likely to be the true transition probability matrix for root caries progression, or a best guess based on the data. The MLE is obtained by summing the two observed transition frequency matrices over two intervals and calculating the row percentage of this matrix.
Pearson Chi-square Tests
The frequency distributions at 18 months, 36 months, and 60 months were predicted using the MLE of transition probability matrix. Due to a limitation in the study data collection time points, the prediction at 60-months was substituted for the actual 54-month (3 cycles) prediction. Thus, the prediction at 60-months was not expected to produce adequate results. The Pearson Chi-square test was used to compare the observed and predicted frequency distributions, i.e., to evaluate goodness-of-fit for our model.
RESULTS
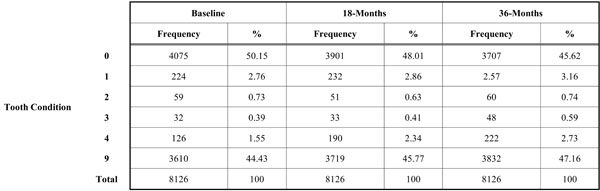
Table 1 displays the observed frequencies of each tooth condition. For each time point, percentages of each tooth condition in the whole population are also presented.
For Each Tooth Condition, the Observed Frequencies and their Contribution to the Whole (%) are Given for Each Time Point
 |
LIKELIHOOD RATIO TEST
The Likelihood Ratio Test compared the transition probability matrix for root caries progression from baseline to 18 months with that from 18 to 36 months. The LRT gives a p-value of 0.0225, which implies that at significance level 0.01, we do not reject the assumption (null hypothesis) that the transition probabilities are constant over different time intervals. Thus, the stationary Markov chain model is valid at the 0.01 level.
MLE of the Transition Probability Matrix
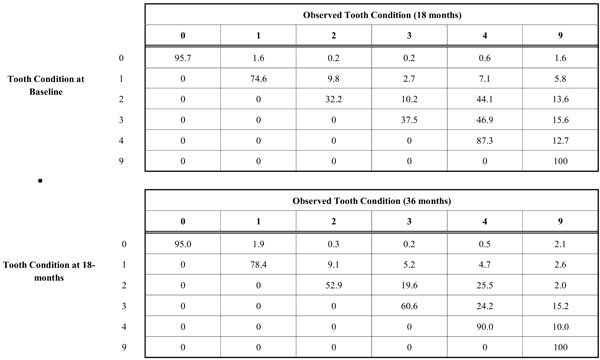
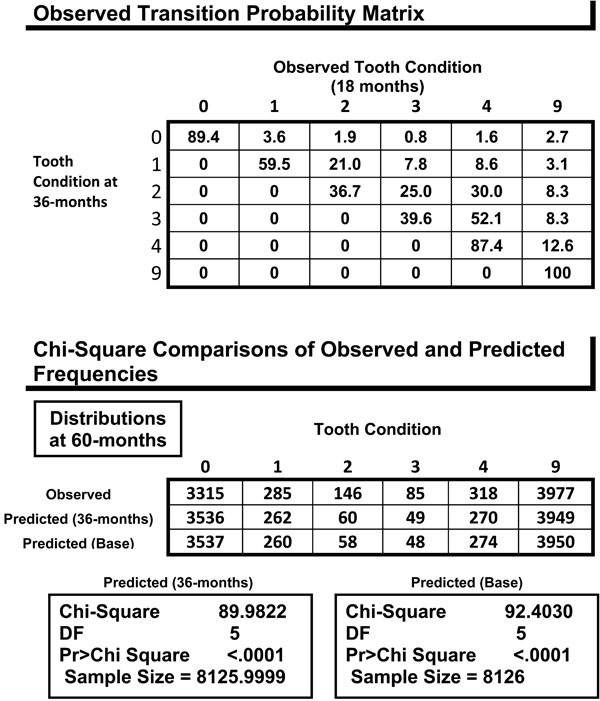
The observed transition probability matrices are presented in Table 2. Each matrix shows progression of the carious process at each time interval. The MLE of the common transition probability matrix is presented in Table 3. The MLE of the common transition probability is a weighted average of the transition probabilities from baseline to 18-months and 18-months to 36-months. The probability of a sound surface progressing toward further destruction and loss is low. But once a lesion is manifested, the probability of additional surfaces to be involved with tooth loss as the ultimate outcome increases. The probability of carious progression increases if a tooth presents with a multi-surface lesion. However, the most stable transitions were the states in which a sound surface (95.4%), 1-surface lesion (76.5%), and a 4-surface lesion (88.9%) remained the same in the next time point; there was a lower probability that these states would develop an additional carious lesion.
The Observed Transition Probability Matrices are Presented for the Time Intervals from Baseline to 18-month and from 18-month to 36-month. A Root Surface that has a One-Surface Lesion can Remain as a Root Surface with a One-Surface lesion (1) or Progress to Develop a 2-surface (2), 3-surface (3), or 4-surface lesion (4), or be missing (9)
 |
The Maximum Likelihood Estimate of the Common Transition Probability Matrix. It is the Basis of the Prediction about the Carious Process
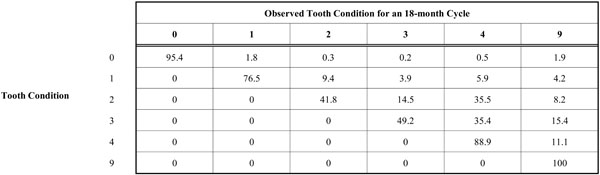 |
From the diagonal of the matrix (Table 3), it can be seen that the probability of a sound surface progressing to a 1-surface lesion is only 1.8%, while the change from a 1 to 2-surface lesion is 9.4%. This is over a 5-fold increase, indicating that a sound tooth surface was least likely to develop a lesion. With multiple infected surfaces, the probability of lesion progression increases, 14.5% for a 2-surface lesion increasing to 3-surfaces and 34.5% for a 3-surface lesion progressing to 4-surfaces. The probability of adding a single lesion to any tooth condition increased as the number of initial lesions increased. The probability of tooth loss was also found to increase with the number of lesions (1.6% to 15.4%), except for the 4-surface lesion where probability of tooth loss markedly declines (11.1%). This appears to emphasize the stability of the 4-surface lesion.
Markov Chain Model Validation
Baseline to 36-Month Data
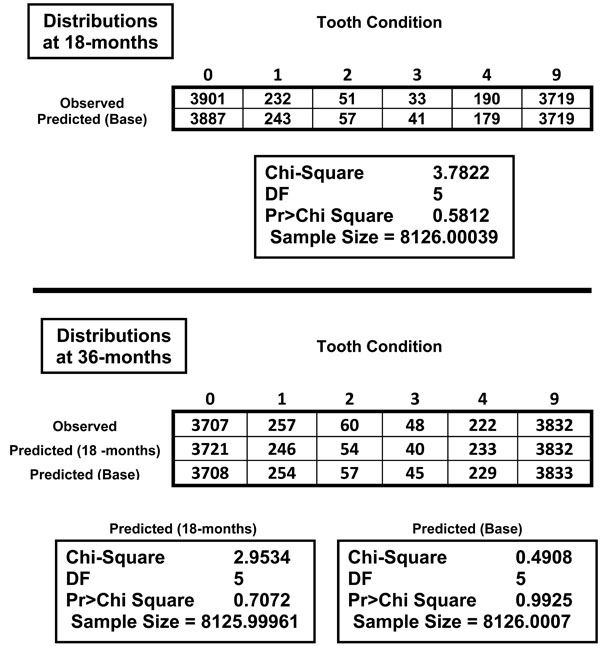
The predicted frequency distribution at 18 months and 36 months were compared to the observed frequency distributions in Table 4. The predicted frequency distributions could be constructed by multiplying a previous observed distribution with a MLE transition probability matrix. For multiple cycles of the model, there was an alternative way to calculate the predicted distribution. The observed distribution at baseline was multiplied by the MLE transition probability matrix several times. The values for the predicted frequency distributions have been rounded off to the nearest integer, similarly for 60-months (Table 5). All the Chi-square tests give p-values greater than 0.5, indicating that there is no statistically significant difference between the observed and predicted distributions. Thus, the prediction with our Markov chain model is successful and valid to 36 months.
The Chi-square Comparisons Indicate that the Goodness of Fit between Observed and Predicted Frequencies is Met at 18-Month and 36-month Time Points
 |
The Chi-square Analysis Indicates that the Observed (60-month) and Predicted (54-month) frequencies are Statistically Different
 |
60-month Data
For the 54-month (3 cycles) prediction, the 60-month time point was used. As expected, the Markov chain model failed to demonstrate a consistent predictive power at the 60-month period as presented in Table 5, due to the difference of 6 months. The predicted frequency distributions demonstrated significant differences from the observed frequency distribution at p <.0001. We did not have data to test the validity of our model past the 36 month interval in predicting the progression of root caries.
DISCUSSION
Since 1907, Markov chain processes have been employed to develop predictor models for use in healthcare and many disciplines, for example, social and behavioral sciences, bioinformatics, economics, and industry [8-10]. In dentistry, the use of Markov models has been advocated and used to predict the health status of teeth and risk for disease [11-14]. Many analytic methods exist to predict outcomes, for example: Regression models, analysis of variance (ANOVA), covariance (ANCOVA) and multiple (MANOVA), generalized additive models, log linear models, and Bayesian processes, to name but a few [15]. Markov models, however, are useful when a decision problem involves risk that is continuous over time, consists of repetitive events, and time dependence of both probabilities and utilities. In other words, a Markov model is a way of representing a changing set of health states over time, where there is known probability or rate of transition from one health state to another. These conditions more accurately represent clinical settings that involve the variable(s) studied. These models are useful in predicting prognoses and probabilities of disease, in this case, caries within populations [13]. In this study, the use of Markov chains was indicated as the analysis of choice to predict the steady state or progression of root caries.
Statistical Significance
The Predictor Model of Root Caries (Predictor Model) that was developed in this study succeeds in describing the progression of root caries lesions using an 18-month predictive cycle. This predictive modeling is valid to 36 months (2 cycles), but lacks the data to test its validity past 36 months. Thus, this model might be valid for many cycles, but we can only validate it for up to 2 cycles due to data limitations.
Further limiting factors in this study include the data set being over 20 years old and dependent on an isolated geographic population. Thus, the results may have limited application to a broader, contemporary population. In addition, the data was collected under the conditions of a field study that inherently have limitations in visualization, lack of professional debridement of the tooth surfaces, and assessment radiographs were not available for caries diagnosis. Whether or not more later stringent methods of caries assessment, similar to criteria set forth by the International Caries Detection and Assessment System (ICADS, 2004), were used, the criteria for assessment of root caries was consistently applied throughout the study. When errors involving scoring inconsistencies and reversals of diagnosis, these were used as exclusionary criteria in developing the data set for this study.
In older adults, the Predictor Model demonstrates that a sound root surface has over 90% probability of remaining caries free. Our data show that once a lesion is present, the Predictor Model indicates that the one and multiple-surface lesions progress aggressively to infect other adjoining tooth surfaces rather than cavitate that infected surface. For the 4-surface lesion, the Predictor Model demonstrates a maturing of the lesion. Thus, the probability of caries progressing to tooth loss is low.
Root caries are empirically shown to progress during a 3 to 6-month period, with particular aggressiveness in medically and dentally-compromised older adults. For the average older adult, an 18-month interval to detect root caries is adequate, particularly when positive attitudes toward dental care and preventive behaviors are maintained. The ability to predict the caries process in older adults over a 3 year period is also adequate. The Predictive Model demonstrates that maintaining sound root surfaces reduces the risk of tooth dysfunction (morphological destruction) and loss. If demineralization occurs, the incorporation of chemotherapeutic agents during the 18-month interval may slow the caries progression process, especially in compromised older adults. Once the lesion is manifested, it will progressively spread to a 4-surface lesion within the 18-month interval. The Predictor Model is useful in emphasizing early treatment intervention, especially for 1 and 2-surface lesions. However, the probability of further infection of multiple surfaces is high if untreated. In addition, treatment options become more complicated and more expensive, and may result in extraction.
Clinical Significance
While the subjects’ preventive and daily oral self-care habits were not documented, the study does provide clinical significance, albeit limited to the population study. Generalization of this clinical significance requires further research from systematic reviews of other current and future published study findings on caries progression and probabilities. Significance is interpreted as caries progression behavior in a 3-year period. In lieu of a set of criteria of parameters that would reflect important therapeutic changes that have clinical relevance to the clinician, significance may be defined as an effect that has meaning in clinical practice [16]. Through clinical experience over a long period of time with local populations, dentists recognize the aggressiveness of dental caries and its deleterious outcomes. This study provides a basis by which quantitative data may be applied to these observations.
Clinical Practice
Dentist may use findings of this study in shared decision-making with patients for determining optimal clinical decision when caries progression is a concern. In this field study of rural older adults, 90% of sound root surfaces remaining caries free over a 3 year period is encouraging. It is also informative to know that once a lesion develops it aggressively infects adjoining surfaces until maturation into the 4-surface lesion, allowing for rehabilitation of lost tooth structure and function. Thus, clinicians would have a basis to discuss prevention and treatment of caries, particularly once evidenced.
CLINICAL PRACTICE GUIDELINE (CPG) – RESEARCHER’S SUMMARY
The Predictor Model of Root Caries predicts the progression of the root caries lesion in older adults over 18-month cycles. This model is valid for two cycles to 36 months, but lacks the data for evaluation past 36 months. A sound root surface shows high probability to remain caries free. However, one and two-surface lesions aggressively infect other adjoining surfaces. Maturing of the carious process occurs with 4-surface lesions, decreasing the probability of tooth loss. The Predictive Model demonstrates that maintaining sound root surfaces reduces the risk of tooth dysfunction (morphological destruction) and loss. Once a lesion is present, early treatment intervention is indicated to reduce the need for more complicated and expensive dental services and prevent tooth loss.
CLINICAL PRACTICE GUIDELINE – CLINICIAN’S SUMMARY
Clinical Question:
For older adults, what is the probability caries will develop on a root surface with or without an existing lesion(s) in a 3-year period?
PIPO Format:
P (Population)=Older adults 65 years of age and older
I (Intervention; condition studied)=Root caries
P (Prediction)=Probability
O (Outcome)=Need for restoration in a 3-year period
Function Category:
Non-institutionalized; Function level not specified in dataset
Significance: Statistical: Established
Clinical: Applicability to practice
Limited – Dataset over 20 years old; Regional population (Iowa)
Established – Posterior probabilities for Bayesian analyses when updating probabilistic data from future studies through translational evidence research (Diagram 1).
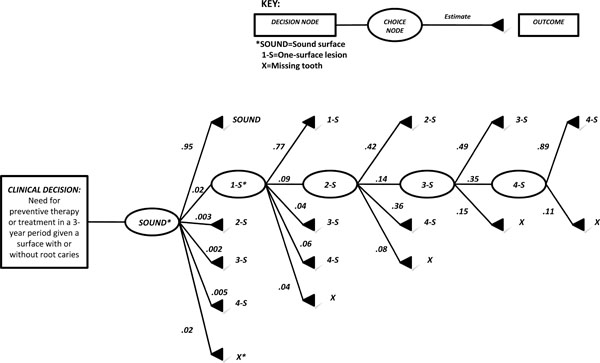
Clinical Practice Guideline - C Clinician’s Summary providing the probability of root caries progression from a sound surface to missing (loss). Other transitions include 1-surface (1-S), 2-surface (2-S), 3-surface (3-S), and 4-surface (4-S) carious lesions.
Provides-Clinician basis for shared decision-making when discussing prevention and treatment of dental caries to patients (Decision analysis provided below).
Meaning in Practice: Undetermined
CLINICAL PRACTICE GUIDELINE – DECISION DATA ONLY
Decision Analysis:
Within 3-years, an older adult may experience a root surface(s) that will either remain in its current health status or proceed to another by the following probability:
A sound surface has a 95% chance of remaining sound and very little chance that it will proceed to a root surface with a carious lesion(s).
A one-surface lesion has a 77% chance of remaining the same and very little chance for caries to involve further surfaces of the same tooth.
A two-surface lesion has a 42% chance of remaining the same, 36% chance of caries involving all 4 surfaces, and 14% chance of involving 3-surfaces.
A three-surface lesion has a 49% chance of remaining the same, 35% chance of caries involving all 4 surfaces and a 15% chance of tooth loss.
A four-surface lesion has an 89% chance of staying the same and 11% chance of tooth loss.
Two and three-surface lesions have greater probability to develop into a 4-surface lesion.


