All published articles of this journal are available on ScienceDirect.
Facial Asymmetry Detected with 3D Methods in Orthodontics: A Systematic Review
Abstract
Background:
Historically, the development of two-dimensional (2D) imaging techniquesforerun that of three-dimensional (3D) ones. Some 2D methods are still considered valid and effective to diagnose facial asymmetry but 3D techniques may provide more precise and accurate measurements.
Objective:
The aim of this work is to analyze the accuracy and reliability of the imaging techniques available for the diagnosis of facial asymmetry in orthodontics and find the most reliable.
Methods:
A search strategy was implemented using PubMed (National Library of Medicine, NCBI).
Results:
A total of 3201 papers were identified in electronic searches. 90 articles, available in full text, were included in the qualitative synthesis consisting of 8 reviews on the diagnosis of facial asymmetry, 22 in vivo and in vitro studies on 2D methods and 60 in vivo and in vitro studies on 3D methods to quantify the asymmetry.
Conclusion:
2D techniques include X-ray techniques such as posterior-anterior cephalogram, which still represents the first level exam in the diagnosis of facial asymmetry. 3D techniques represent the second level exam in the diagnosis of facial asymmetry. The most current used techniques are CBCT, stereophotogrammetry, laser scanning, 3D optical sensors and contact digitization. The comparison between bilateral parameters (linear distances, angles, areas, volumes and contours) and the calculation of an asymmetry index represent the best choices for clinicians who use CBCT. The creation of a color-coded distance map seems to represent the most accurate, reliable and validated methods for clinicians who use stereophotogrammetry, laser scanning and 3D optical sensors.
1. INTRODUCTION
Clinically, “symmetry” is synonymous with balance, while “asymmetry” refers to a difference between homologous elements in which the harmonic relationship among structures is altered [1]. The observation of facial or dental asymmetry in patients, both mild or severe, is a common and important finding. It is frequent because perfect symmetry of the body is extremely rare and primarily it remains a theoretical concept. It is important because most recent anthropological researches reveal that symmetry is fundamental in order to increase the charm of human face [1-5].
Literature lacks a comprehensive definition of facial asymmetry [6-12]. According to Bishara [6], for example, it corresponds to “differences in the size or relationship between the two sides of the face”. According to Beyer [8], it is “a lack of coincidence between maxillary and mandibular midlines as well as the facial soft-tissues midlines”. Kwon [12] claims that patients with facial asymmetry are distinguished by a chin deviation greater than 4 mm from the facial midline.
Epidemiological studies estimated that facial asymmetry in orthodontic patients has a prevalence of around 12 to 37% in the USA [13-15], 23% in Belgium [16], and 21% in Hong Kong [17] if the diagnosis is clinical. On the other hand, if the diagnosis is based on radiological findings, the prevalence may exceed 50% [18, 19].
Regarding the diagnosis, there are multiple methods available for clinicians to identify and assess facial asymmetry [5, 10, 11, 20-24]. Historically, the development of two-dimensional (2D) imaging techniques, such as panoramic radiographs, posterior-anterior cephalograms and photographs, forerun that of three-dimensional (3D) ones, which included CBCT, stereophotogrammetry, laser scanning and contact digitalization [22]. 3D techniques represent a fundamental advancement for improving our knowledge of facial asymmetry [25], and they may provide more precise and accurate measurements [22]. However, some 2D methods are still considered valid and effective in diagnosing facial asymmetry [22].
Each method varies in accuracy, reliability, biologic and economic costs. Furthermore, it is important to identify the most appropriate diagnostic tool for each clinical case, as errors during the diagnostic phase could lead to misinterpretation of the asymmetry and they may limit treatment options. Therefore, the aim of the present review was to analyze the accuracy and reliability of the imaging techniques available for the diagnosis of facial asymmetry in orthodontics and find the most reliable.
2. MATERIALS AND METHODS
A literature search with “facial asymmetry”, “diagnosis”, “2D diagnosis” and “3D diagnosis” keywords was conducted on PubMed (National Library of Medicine, NCBI) on articles published from 1994 to 2020 in English and in Italian and available in full text (last access on 30th April 2020). This restricted time span was chosen considering that, with the rapid technological evolution of diagnostic instruments, a greater homogeneity of analyzed tools that are still in use is more suitable for finding useful suggestions for contemporary practice compared to a broader historic review. These studies concern facial and/or mandibular asymmetry (not regarding more limited investigation field like, for example, condylar asymmetry only), they have been performed on patients or cadavers and they present detailed documentation relating to the selection of subject, image processing and calculations performed to quantify asymmetry.
Therefore, the various methods used to diagnose facial asymmetry were extrapolated. Another database search was performed using “clinical examination”, “panoramic radiograph”, “posterior-anterior cephalometry”, “digital photography”, “CB-CT”, “stereophotogrammetry”, “laser scanning”, “3D optical sensor” and “contact digitalization” keywords. Subsequently, the terms of the second search were combined with the first ones in order to reduce irrelevant results and finally the bibliographies of the extrapolated studies were analysed in order to offer the widest possible overview of the available methods.
3. RESULTS
3.1. Study Selections
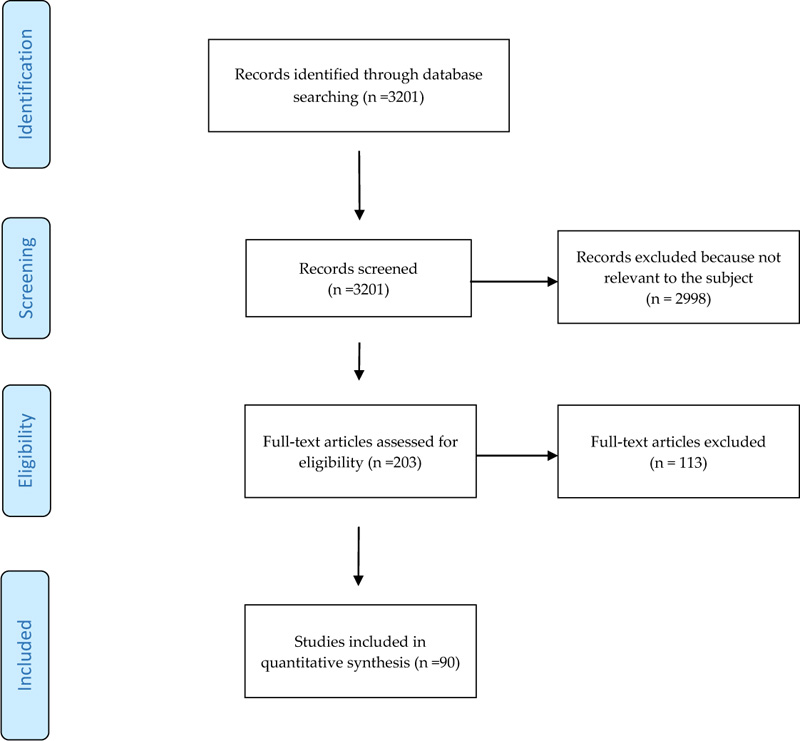
The initial research led to the identification of 3201 articles, the majority of which were excluded after reading the abstracts because they were not relevant to the topic of this study or inaccessible. 90 articles, available in full text, were included in the qualitative synthesis, which consisted of 8 reviews [5, 6, 10, 24-28] on the diagnosis of facial asymmetry, 22 in vivo and in vitro studies on 2D methods and 60 in vivo and in vitro studies on 3D methods for quantifying asymmetry. The articles selection process is illustrated through the PRISMA flow diagram presented in Fig. (1).
3.2. Results of Studies
Clinical examination shows the presence of sagittal, coronal and vertical asymmetry and is divided into an extra-oral and an intra-oral examination [10, 11, 22-24, 26]. To enhance asymmetry investigation clinicians can use two and three-dimensional techniques.
3.3. Two-Dimensional Techniques
Two-dimensional techniques, summarized in Table 1, include radiological techniques such as posterior-anterior cephalogram (PA cephalogram), which still represents the first level exam in the diagnosis of facial asymmetry, panoramic radiography (OPG) and submentovertex projection [5, 6, 11, 22, 24, 29]. The latter is no longer used in the daily routine because it exposes patient’s thyroid to an important dose of radiations, it forces the patient to assume an uncomfortable position during the examination and there is the superimposition of different anatomical structures that result in a lower accuracy compared to other methods [22, 27]. OPG is also rarely used for this objective in clinical practise as it is affected by many disadvantages like distortion and magnification of radiographed structures and limitation of diagnosis to condyle and mandibular ramus asymmetry [22, 27, 28]. Digital photography represents a valid two-dimensional non-radiographic technique for the diagnosis of facial asymmetry [29, 30]. It completes the clinical evaluation and makes it more accurate. The frontal view is the most useful to analyses patient’s asymmetry [5, 22].
| Study | Techniques Used |
Use of Reference Lines |
Number of Landmarks |
Methods to Quantify the Asymmetry | Aim of the Study |
|---|---|---|---|---|---|
| Altug-Atac (2008) | PA cephalogram and digital photography |
Yes | 13 | Comparison between bilateral distances | To investigate the relationship between soft-tissue and underlying skeletal structures before and after unilateral mandibular distraction osteogenesis |
| Baudouin (2004) | Digital photography |
Yes | 53 | Calculation of an asymmetry index (linear) | To investigate female facial attractiveness by comparing the ratings made by male judges with the metric characteristics of female faces |
| Danel (2007) |
Digital photography |
No | 2 | Comparison between left and right part of eye-mouth-eye angle | To test the hypothesis that men with more masculine values of EME angle and/or more symmetrical values would be perceived by women as more attractive |
| Edler (2001) |
Digital photography |
No | 6 | Comparison between areas, perimeters and moments of the inferior half-face | To investigate assessment of mandibular asymmetry by clinicians and to evaluate a new computerized system |
| Edler (2003) |
PA cephalogram and Digital photography |
No | 4 | Comparison between bilateral areas, perimeters, compactness (shapes) and moments of the inferior third of face |
To assess asymmetry analysis of PA radiographs as a method for mandibular asymmetry measurement and to compare it with the digitization of mandibular outlines from facial photographs |
| Ercan (2008) |
Digital photography |
(Yes) | 42 | Calculation of Euclidean distance matrix analysis* | To quantify asymmetry between the right and the left parts of the face |
| Eskelsen (2009) | Digital photography |
Yes | 2 | Evaluation of coincidence or not between bipupillar bisector line and dental midline | To analyze the axial symmetry between the bipupillar midline and the maxillary central incisors midline |
| Fong (2010) |
PA cephalogram |
Yes | 14 | Comparison between bilateral distances to reference lines | To investigate the facial skeletal features associated with chin deviation |
| Good (2006) |
Lateral cephalogram and Digital photography |
Yes | 10 | Comparison between bilateral areas, perimeters, compactness (shapes) and moments of the inferior third of face | To investigate the relationship between mandibular outline asymmetry and skeletal discrepancy |
| Gosla-Reddy (2011) | Digital photography |
Yes | Not well defined |
Comparison between areas, bilateral distances and angles | To assess and compare nasal symmetry in patients who underwent correction of a complete unilateral cleft lip |
| Grammer (1994) | Digital photography |
No | 13 | Calculation of an asymmetry index (linear) | To investigate if men and women prefer averageness and symmetry in faces |
| Haraguchi (2002) | PA cephalogram and Digital photography |
Yes | 7 | Comparison between landmarks' bilateral distances to the reference lines, subjective assessment of asymmetry | To investigate the frequency, site, amount, and direction of facial asymmetry in human adults with mandibular prognathism and examined if these characteristics were associated postnatally with cardinal clinical signs that may indicate a predisposition to facial asymmetry |
| Hwang (2007) |
PA cephalogram and Digital photography |
Yes | 11 | Evaluation of seven measurements (bilateraldistances, angles) on PA cephalogram and one on digital photography | To classify patients with facial asymmetry by using the cluster analysis |
| Kjellberg (1994) | Panoramic radiograph |
No | 6 | Comparison between bilateral distancesand “condylar ratio” | To develop and apply a reliable method of measuring the effects of condylar lesions quantitatively on panoramic radiographs |
| Nakamura (2001) | PA cephalograms and Digital photography |
Yes | 18 | Calculation of an asymmetry index (linear) | To compare the asymmetry of the facial skeleton or expression of such patients with those of healthy subjects |
| Penton-Voak (2001) | Digital photography |
No | 14 | Ratings of similarity between mirrored faces, evaluation of horizontal/vertical asymmetry from x-y coordinates of bilateral points, digital averages (composite) of multiple individual faces |
To demonstrate that symmetric faces are more attractive than less symmetric ones |
| Rikowsky (1999) | Videocamera (snapshots that showed the best positions) |
No | 13 | Calculation of an asymmetry index (linear) | To compare ratings of body odor, attractiveness, and measurements of facial and body asymmetry |
| Saglam (2004) |
Panoramic radiograph |
No | 4 | Calculation of an asymmetry index (linear) | To examine the relation of condylar asymmetry index in dentate patients with TMD |
| Scheib (1999) |
Digital photography |
Yes | 14 | Calculation of an asymmetry index (linear) | To examine women’s perception of facial attractiveness and symmetry |
| Trpkova (2003) |
PA cephalogram |
Yes | 44 | Comparison between landmarks' bilateral distances to the reference lines | To determine the ability of various horizontal and vertical reference lines to provide measurements of dentofacial asymmetries from PA cephalograms |
| Yamashita (2009) | PA cephalogram and digital photography |
Yes | 9 | Comparison between bilateral landmarks’ distances to reference lines, comparison between areas | To examine labial asymmetry in patients with jaws’ deformity and facial asymmetry |
| Yu (2009) |
Digital photography |
Yes | 7 | Calculation of an asymmetry index (angular) | To determine whether the technique used in the study can improve the midline symmetry of facial soft tissues |
3.4. Three-Dimensional Techniques
In respect of 3D radiographic techniques, clinicians use cone-beam computed tomography (CBCT) to evaluate asymmetry creating three-dimensional virtual models from it [12, 31-33]. Stereophotogrammetry, laser scanners, 3D optical sensors and contact digitalization represent the 3D non-radiographic counterparts [34-36]. Table 2 presents an overview of studies quantifying the asymmetry through 3D techniques.
Cone-beam images are not characterized by tissues and organs superimposition and allow the exact definition of structures in three dimensions [22]. The patient positioning during the examination is critical in this technique as well as in other 3D and 2D ones [37].
Stereophotogrammetry is used in measuring two or more photographic images taken from different positions in order to realize a 3D reconstruction of his/her facial soft tissues according to a stereoscopic vision using triangulation concepts [38-40]. The outcome is a sort of scan (but without the use of scanner) of the patient’s face. This technique affords obtaining a precise and realistic rendering of the facial surface [34, 41].
| Study | Techniques Used | Use of Reference Planes | Number of Landmarks | Methods to Quantify the Asymmetry | Aim of the Study |
|---|---|---|---|---|---|
| Al-Rudainy (2018) | Stereo-photogrammetry | Yes | 25 | Creation of a color-coded map (based on absolute distances between original and mirrored images superimposed) | To evaluate facial asymmetry before and after surgical repair of cleft lip in infants |
| Alqattan (2015) | Laser scanning | Yes | 21 | Calculation of a landmark-based asymmetry index (according to Huang) and carrying out a surface-based asymmetry analysis with the creation of mirrored images | To collect the reference values for facial asymmetry in adults using landmark and surface-based three-dimensional analyses and to compare their diagnostic abilities |
| An (2017) |
CBCT | Yes | 11 | Calculation of the horizontal distance from the reference planes to menton and ANS and the angles between the reference planes and the line passing through ANS and PNS | To compare eight candidate midsagittal planes constructing from different median landmarks to determine the most appropriate one for evaluating craniofacial asymmetry |
| Baik (2010) |
Laser scanning | Yes | 31 | Creation of a color-coded distance map based on the scans superimposed, evaluation of points coordinates changes (69 linear, 8 angular, 13 proportional measurements) | To use a 3D laser scanner to evaluate the soft-tissue changes after the correction of skeletal Class III malocclusions with orthognathic surgery |
| Benz (2002) |
3D Optical sensor | Yes | 2 | Determination of the symmetry plane after registration between original and mirrored images | To present an application of optical metrology and image processing to oral and maxillofacial surgery |
| Berssenbrugge (2014) | Stereo-photogrammetry Digital photography |
Yes | 22 | Calculation of 2D asymmetry index (according to Nakamura, Badouin and Grammer) and 3D asymmetry index (starting from the superimposition between original and mirrored images) | To compare three selected 2D analysis methods and one 3D analysis method |
| Bilwatsch (2006) | 3D Optical sensor | Yes | 25 | Calculation of the distances of the landmarks from the plane of symmetry and in postero-anterior direction, comparison between virtual volumes of the face and angles | To assess the degree of facial asymmetry in patients suffering from unilateral cleft lip, alveolus and palate |
| Bugaighis (2014) | Stereo-photogrammetry | No | 39 | Calculation of the distances between each landmark and the matching reflected landmark | To explore 3D facial asymmetry differences in operated children with oral clefts and to compare the results with a control group |
| Cassi (2018) |
Stereo-photogrammetry | Yes | 16 | Creation of a color-coded distance map (based on calculation of RMSE* on the original and mirrored images superimposed) | To quantify the surface of facial asymmetry in a group of young patients with hemifacial microsomia and to investigate differences with a homogeneous sample of healthy subjects |
| Cevidanes (2011) | CBCT | Yes | 3 | Creation of a color-coded distance maps (magnitude of the differences between the mirror and simulated asymmetry point-based models) | To determine if 3D shape analysis precisely diagnoses right and left differences in asymmetry patients |
| Claes (2011) |
Stereo-photogrammetry | Yes | 2 | Creation of color-coded map based on distances between original and mirrored spatially-dense quasi-landmarks | To obtain robust and spatially-dense asymmetry assessments using a superimposition protocol for comparison of a face with its mirror image |
| Codari (2017) |
Stereo-photogrammetry | No | 29 | Creation of a color-coded map of distances (based on calculation of RMSD ** on the original and mirrored images superimposed) | To present a new quantitative method to assess symmetry in different facial thirds |
| Damstra (2011) | CBCT | Yes | 21 | Comparison between bilateral linear and angular measurements (including Hwang's ones), creation of a color-coded map based on distances between original and mirrored (midsagittal plane, half) images superimposed | To illustrate and discuss the method of mirror-image analysis in addition to the quantitative 3D analysis of asymmetry with a case report |
| Damstra (2012) | CBCT | Yes | 40 | Determination of the true midsagittal plane after superimposition of reflected models | To investigate if the cephalometric midsagittal planes using internal and midline structures are relevant to visible facial symmetry |
| Demant (2011) |
Stereo-photogrammetry | No | 22 | Creation of a color-coded map based on distances between original and mirrored images superimposed | To investigate and compare facial asymmetry in subjects with JIA with unilateral, bilateral or no TM joint involvement |
| Djordjevic (2014), (2013) | Laser scanning | Yes | 21 | Creation of a color-coded map and an histogram to explain original shell-mirrored shell deviation, comparison between bilateral distances and angles | To explore facial symmetry in healthy growing individuals and determine whether asymmetric changes occur during adolescent growth |
| Economou (2018) | CBCT Stereo-photogrammetry |
Yes | 38 | Comparison between bilateral distances to the reference planesand between bilateral gonialangles | To assess the correlation between facial hard and soft tissue asymmetry in patients with juvenile idiopathic arthritis, to identify valid soft tissue points for clinical examination, and to assess the smallest clinically detectable level of dentofacial asymmetry |
| Ekrami (2018) |
Laser scanning | No | 19 | Creation of a color-coded map (based on distances between original and mirrored spatially-dense quasi-landmarks) | To perform a simulation study to illustrate the performance and benefit of spatially dense and automated approach in calculating fluctuating asymmetry over the traditional use of sparse landmarks |
| Ferrario (2003) |
Contact digitalization | No | 11 | Calculation of linear distances, angular measurements, areas and volumes | To measure the difference between adult patients operated on for cleft lip and palate and healthy adults in an attempt to provide a final assessment of the facial outcome of surgery |
| Hajeer (2004) |
Stereo-photogrammetry | No | 19 | Comparison between the patient’s original configuration and the symmetrical one | To assess the magnitude of 3D asymmetry of facial soft tissues before and after orthognathic operations |
| Hartmann (2007) | 3D Optical sensor | Yes | None | Determination of the symmetry plane (starting from the superimposition between original and mirrored images) and creation of a color-coded distance map | To analyze the reliability of a landmark-independent method for determining facialsymmetry |
| Hennessey (2006) | Laser scanning | No | 24 | Calculation of the asymmetry vector for each subject produced by subtracting the coordinates of the mirrored configuration of landmarks from the original configuration | To examine covariance of facial shape and asymmetry with cognition in a normal sample |
| Hood (2003) |
Stereo-photogrammetry | No | Not defined | Calculation of an asymmetry index based on the mean distances between original and mirrored configurations of landmarks superimposed | To determine the degree of facial asymmetry in infants with unilateral cleft lip and/or palate, and 3D quantify improvements following primary surgery |
| Huang (2013) |
Stereo-photogrammetry | Yes | 16 | Calculation of an asymmetry index | To differentiate a symmetric face from an asymmetric face by analyzing a three-dimensional facial image |
| Hwang (2006) |
CBCT | Yes | 21 | Comparison between six “dimensions” (bilateral distances and bilateral angles) | To describe the use of 3D images in the diagnosis of facial asymmetry |
| Kamata (2017) |
CBCT | Yes | 14 | Calculation of linear and angular measurements, comparison between subjects with and without facial asymmetry | To elucidate the factors that cause facial asymmetry by comparing the characteristics of the mandibular morphology in patients with mandibular prognathism with or without facial asymmetry |
| Katsumata (2005) | CBCT | Yes | 22 | Calculation of a linear asymmetry index | To test a 3D coordinate point evaluation system to assess and diagnose patient with facial asymmetry |
| Kornreich (2016) | Stereo-photogrammetry | Yes | 10 | Creation of a color-coded map and histogram (based on RMS*** calculated on the original and mirrored images superimposed) and comparison among linear distances | To compare of global versus landmark analyses of facial asymmetry using 3D photogrammetry |
| Kwon (2006) |
CBCT | Yes | 34 | Comparison between bilateral distances and angles, left-right differences between the distances of each bilateral points to the reference planes | To evaluate the morphological characteristics of the cranial base and the maxillomandibular structures of facial asymmetry in adult patients |
| Kwon (2019) |
CBCT | Yes | 24 | Comparison between bilateral linear and angular measurements | To investigate morphologic differences between the ipsilateral and contralateral types of facial asymmetry |
| Leung (2018) |
CBCT | Yes | 38 | Performing of a 3D cephalometric analysis | To propose a new classification of mandibular asymmetry by anatomical regions |
| Maeda (2006) |
CBCT | Yes | 21 | Calculation of an asymmetry index (according to Katsumata) | To characterize the symmetrical features of patients with facial deformities and to suggest a classification system for facial asymmetry based on 3D computed tomography evaluation |
| Meyer-Marcotty (2011) | 3D Optical sensor | Yes | None | Determination of the symmetry plane and generation of facial asymmetry through virtual incremental alteration | To analyze the perception of various degrees of facial asymmetry |
| Moro (2009) |
CBCT, PA cephalograms | Yes | 3 | Comparison between bilateral distances to the reference plane | To compare a computed tomographic three- dimensional analysis with a model analysis to use it as diagnostic aid for the evaluation of occlusal plane tilting in facial asymmetry |
| Nkenke (2006) |
3D Optical sensor | Yes | 26 | Determination of the symmetry plane, comparison between bilateral distances, virtual volumes and angles | To assess measurement errors of a novel technique for the 3D determination of the degree of facial symmetry in patients suffering from unilateral cleft lip and palate malformations |
| Nur (2016) |
CBCT | Yes | 22 | Comparison between bilateral linear, surface distance, angular, volumetric, and surface area measurements | To evaluate facial asymmetry three-dimensionally using CBCT and compare the right and left facial hard and soft tissues volumetrically and their interferences on each other |
| O’Grady (1999) | Laser scanning | Yes | 26 | Calculation of Euclidean distance matrix analysis (landmarks) and clearance vector (distance between superimposed surface), comparison between bilateral surface contour, surface areas, volumes | To evaluate six different techniques with respect to their ability to quantitatively describe facial asymmetry |
| Ostwald (2015) |
3D Optical sensor | Yes | None | Calculation of an asymmetry index (average distance between original and reflected surface), creation of a color-coded map and histogram (based on the asymmetry index values), use of a visual analog scale to rate symmetry (subjective rating) | To answered different questions: is symmetry an appropriate value to describe facial variations? Is there a correlation between rated symmetry and attractiveness scores? Is there a correlation between (objective) (a)symmetry and rated (subjective) symmetry? |
| Ozsoy (2016) |
Laser scanning (hand-held scanner) | Yes | 11 | Creation of a color-coded distance maps (based on calculation of RMS, MAD1, MSD2 on the original and mirrored images superimposed) | To analyze the global and partial asymmetry of facial soft tissues using three different calculation methods and investigate the relationships among them |
| Park (2012) |
CBCT | Yes | 12 | Comparison between the bilateral distances of the reference points from the reference planes | To characterize symmetrical features of patients with facial asymmetry and thus to find the most reliable horizontal reference lines easily used in 3D images |
| Patel (2015) |
Stereo-photogrammetry | Yes | None | Creation of color-coded facial map and histogram starting from the superimposition between the original and mirrored images | To develop a technique to automatically localize and quantify soft-tissue asymmetry in adults using 3D facial scans |
| Pinheiro (2019) | CBCT | Yes | 25 | Performing of a3D cephalometric analysis | To evaluate a protocol for 3D cephalometric analysis for both the identification of the natural head position and the accurate quantification of facial growth and facial asymmetry is proposed and evaluated |
| Primozic (2012) | Laser scanning | Yes | 2 | Creation of a color-coded deviation map based on theaverage distances between mirrored images, determination of the predominance of either the left or right side of the face for each part of the face separately | To evaluate facial asymmetry in growing subjects with nomalocclusion on 3D laser facial scans |
| Ras (1995) |
Stereo-photogrammetry | Yes | 26 | Calculation of the spatial distance of the minimal movement XY’ to attain a symmetrical arrangement of the bilateral landmarks X and Y to the sagittal | To describe 3D developmental changes of facial asymmetry in children with an operated complete unilateral cleft lip and palate and in children without craniofacial anomalies |
| Sanders (2014) |
CBCT | Yes | 38 | Comparison between bilateral distances | To identify and quantify the characteristics of facial and dental asymmetries in a normal, adolescent population using 3D images |
| Schwenzer-Zimmerer (2008) | Laser scanning | Yes | 16 | Creation of a color-coded distance map based on the scans superimposed, comparison between six pre and post treatment variables | To evaluate the clinical application of 3D imaging to analyze symmetry in cleft and non-cleft persons |
| Sforza (2007) |
Contact digitalization | Yes | 50 | Calculation of a linear asymmetry index | To compare skeletal class III patients with normal subjects in the field of facial asymmetry |
| Shaner (2000) |
Stereo-photogrammetry | Yes | 28 | Comparison between distances between two landmarks, angles between two landmarks and the horizontal plane, and depths;calculation of 3D coordinates of the landmarks and the coordinate direction angles of the landmarks |
To determine if facial asymmetry was greater in syndrome-affected individuals than in normal individuals |
| Shin (2016) |
CBCT | Yes | 34 | Calculation of the distances between the median cephalometric landmarks and the individual symmetric midsagittal reference plane | To determine, by statistical shape analysis of original and mirrored skeletal landmarks, the optimal landmark-based midsagittal reference plane for evaluation of facial asymmetry |
| Sievers (2012) |
CBCT | Yes | 22 | Calculation of an asymmetry index (according to Katsumata) | To estimate possible differences in skeletal asymmetry between patients with skeletal Class I and skeletal Class II relationships |
| Stauber (2008) |
3D Optical sensor | Yes | 26 | Comparison between bilateral distances, virtual volumes and angles (Nkenke’s method) | To present a new technique to determine the plane of symmetry of a face, and to assess the degree of facial symmetry in patients with unilateral cleft lip |
| Taylor (2014) |
Stereo-photogrammetry | No | None | Creation of a color-coded distance map (based on calculation of RMSD on original and reflected images superimposed) | To demonstrate a method for reproducibly and rapidly calculating a single number value for facial surface symmetry with a plane of maximum symmetry |
| Verhoeven (2013) | Stereo-photogrammetry | Yes | 6 | Creation of a color-coded distance map based on absolute mean distances between original and mirrored images superimposed | To introduce and validate a new method that quantifies soft-tissue facial asymmetry in patients who have undergone mandibular reconstruction |
| Verhoeven (2016) | Stereo-photogrammetry | Yes | 19 | Creation of a color-coded distance map based on the absolute mean distance between the original and mirrored images | To compare the validity and reproducibility of four different methods for the quantification of soft tissue facial asymmetry |
| Wermker (2014) | Stereo-photogrammetry | Yes | 12 | Calculation of an asymmetry index (mean of all distances between original and mirrored dataset superimposed) andcreated of a false-color map | To document and analyze the results of orthognathic surgery, to assess the soft tissue response relatedto the skeletal shift and the alterations in facial symmetry after orthognathic surgery |
| Wong (2014) |
CBCT | Yes | 4 | Determination of the voxel-based optimal plane ofsymmetry | To introduce a new method of planning surgical correction of facial asymmetry using the OSPs as guides and test its effectiveness |
| Yanez-Vico (2011) | CBCT | Yes | 14 | Calculation of a linear asymmetry index, six Hwang’s dimensions | To use 3D reconstructions of computed tomography to evaluate facial asymmetry |
| Yanez-Vico (2013) | CBCT | Yes | 31 | Comparison between bilateral distances and between normal and not normal subjects’ cephalometric measurements (maxillary, mandibular and dento-alveolar) | To introduce a new three-dimensional analysis of clinical value for evaluating asymmetry in cases of craniofacial syndrome |
| Yang (2016) |
CBCT | Yes | 26 | Calculation of an asymmetry index (linear) | To examine facial asymmetry in patients with unilateral cleft lip and palates |
| You (2018) |
CBCT | Yes | 25 | Comparison between bilateral distances and angles | To analyze the morphologic features of skeletal units in the mandibles of patients with facial asymmetry and mandibular retrognathism |
Laser scanner emanates an electromagnetic impulse (the “laser”) and receives the reflected signal, calculating time lapse passed and subsequently the distance between the instrument and the detected point. Data acquisition permit to obtain several points that define the object or subject surface and that are reworked in 3D models of the patient [34, 42].
3D optical sensors fall into the category of structured light techniques, such as stereophotogrammetry. They are based the triangulation principles, as well described by Kau [34] as follows. “Normally, a projector shines a pattern of ‘structured’ light (which may be composed of elliptical patterns, random texture maps, etc.) onto a targeted surface to be scanned. When the light illuminates the surface, the light pattern distorts and bends. A system of cameras at a known distance captures the reflected and distorted pattern under an angle and translates the information into 3D coordinates” [34].
Contact digitalization uses direct contact with the subject to obtain a 3D-dimensional reconstruction of the patient’s surface, based on single points. This means that the patient’s face becomes a framework and not a complete model where only landmarks are rebuilt, and not the complete surface of the face [43].
4. DISCUSSION
The observation of facial or dental asymmetry in patients, both mild or severe, is an important finding because symmetry and averageness are fundamental in order to increase facial aesthetics. There are different techniques to identify facial asymmetry to support clinical examination, mainly divided into 2D and 3D techniques.
4.1. Two-Dimensional Techniques
Two-dimensional techniques can be considered as first-level exams in the diagnosis of facial asymmetries. In particular, posterior-anterior cephalogram is the most commonly used radiograph to detect this kind of problem, despite it is characterised by limits and errors [22, 24]. For example, in Yanez-Vico’s systematic review on facial asymmetry (2010) [22] it is reported that a simple head rotation can modify the perpendicularity of cranial middle sagittal line in relation to the x-ray, leading to falsified calculations. Moreover, median sagittal line identification can be extremely difficult in patients affected by severe asymmetries. Trpkova [44] and Legrell [45] outline two recurrent errors in posterior-anterior cephalogram: those connected to cephalometric method (head rotation and object-film distance) and those inherent to the method itself (identification of landmarks and superimposition of anatomic structures). PA cephalogram remains a bidimensional representation of 3D structures and provides limited information about vertical and posterior-anterior dimensions. However, facial asymmetry distorts cephalometric measurements both in 2D and 3D [37]. In addition to these limits, Mayor [46] outlines the need to use “reliable localization” landmarks (i.e. landmarks with intra and inter-examiner variation less than 1.5 mm) in order to reduce the second type of errors existing in posterior-anterior cephalogram. PA cephalogram exposes patients to a low dose of radiation as compared to its radiographic 3D counterparts. As regards the non-radiographic counterpart, digital photography completes clinical examination and makes it more accurate but, once again, it is a bidimensional representation of tridimensional structures. Both posterior-anterior cephalogram and digital photography are simple to learn and low-cost techniques.
In view of the above-mentioned advantages and disadvantages, the problem to quantify facial asymmetry through these techniques remains. According to Berlin’s systematic review [5] the most recommended methods are those that calculate facial asymmetry index. Nakamura [47], Baudouin [48] and Grammer [49] quantify asymmetry by means of a numerical parameter that allow the subsequent comparisons among patients. However, this unique measurement provides little or no information on the part of the face mainly being disharmonic. Clinicians may need to carry out analysis on a smaller scale to analyse small facial areas, to measure single angles and areas as well as to calculate more than one asymmetry index (possibly adding them in a total facial asymmetry index), in order to identify the components responsible for the facial disharmony. Yu [50] exposes ideal diagnostic methods requirements for facial asymmetry: it has to be simple to use without long training in landmarks identification, simple to understand and communicate to patients, cheap and characterized by minimal and essential number of measurements. According to Yu’s recommendations, Baudouin’s method [48] implicates an excessive number of landmarks (53), in contrast to Nakamura and Grammer’s ones [47, 49]. All three methods are cheap and used landmarks are simple to identify. Nakamura and Baudouin analyse both hard and soft tissues and provide a fuller vision, etiologically speaking, of the asymmetry. Several authors do not calculate any asymmetry index. Above all, they measure and compare bilateral distances, generally starting from the identification of reference points and lines [18, 34, 44, 51-57]. Therefore, their analysis focuses on the disharmony of the individual elements without calculating an asymmetry index that allows to quantify the facial imbalance in a simpler and a more immediate way. One author deviates from Yu's recommendations as he identifies many landmarks [44]. On the contrary, most of them foresee from a minimum of 2 to a maximum of 14 reference points in their studies [55, 58].
| Two-Dimensional Techniques to Diagnose Facial Asymmetry | |||
|---|---|---|---|
| Types of Techniques | OPG | PA Cephalogram | Digital Photography |
| Advantages | Panoramic vision of teeth and jaws; low dose of radiation. | First level exam in the diagnosis of facial asymmetry; low dose of radiation. | Useful for soft-tissue asymmetry analysis |
| Disadvantages | Distortion; magnification; diagnosis limited to condyle and mandibular ramus asymmetries; 2D vision of 3D structures. | Distortion; magnification; superimposition of anatomical structures; 2D vision of 3D structures. | 2D vision of 3D structures |
| Methods to quantify the asymmetry | Calculation of an asymmetry index; comparison between bilateral distances. | Calculation of an asymmetry index; comparison between bilateral distances and areas; performing of a cephalometric analysis; evaluation of the coincidence between two lines. | Calculation of an asymmetry index; comparison between bilateral distance,angles and areas; calculation of EDMA*; ratings of similarity between mirrored faces |
| Three-Dimensional Techniques to Diagnose Facial Asymmetry | |||||
|---|---|---|---|---|---|
| Types of Techniques | CB-CT | Stereophotogrammetry | Laser Scanning | 3D Optical Sensors (Computer-Aided Structured Light) | Contact Digitalization |
| Advantages | 3D vision of structures; lack of superimposition; measurements accuracy. |
Realistic and accurate rendering of the face surface easy to set up. | High resolution; medium photorealistic quality; acquisition of contour, topology and surface data; existence of low-cost scanner. | Photorealistic rendering of the face surface; very rapid capture. | Non-invasive. |
| Disadvantages | More expensive and higher dose of radiation than 2D radiographic methods; artefacts. | Initial training; suitable and expensive equipment; inaccurate rendering of some parts (like hairs); magnification errors; tedious work to map surfaces. |
Remarkable duration (need of patient stillness); initial training; suitable equipment. | Variable resolution quality; sensitive to the technique. | Initial training; remarkable duration; suitable equipment; face recreation through points that outline the surface. |
| Methods to quantify asymmetry | Calculation of an asymmetry index; comparison between bilateral distances, angles and volumes; creation of a color-coded distance map; determination of the plane of symmetry; performing of a 3D cephalometric analysis. | Creation of a color-coded distance map; calculation of an asymmetry index; comparison between bilateral distances; comparison between the patient's original configuration and the symmetrical one. | Creation of a color-coded distance map; comparison between bilateral distances, angles, areas, volumes and contours; calculation of an asymmetry index or an asymmetry vector. | Determination of the plane of symmetry; comparison between bilateral distances, angles and volumes; creation of a color-coded distance map; calculation of an asymmetry index. | Calculation of an asymmetry index; comparison between bilateral distances and angles |
About landmarks and reference lines, most authors use points validated by the literature, such as the ones easier to identify and the ones their localization is subjected to fewer errors, following in particular Farkas' studies [59, 60]. The methods used are relatively simple to communicate and share with patients, in particular, if based on a limited number of reference points and measurements, such as those stated in the findings of Edler [61], Danel [55], Eskelsen [62], Saglam [63]. The two-dimensional techniques are cheaper than the three-dimensional ones both with reference to the execution costs of a photograph, an OPG or a PA cephalogram and with reference to the software necessary to carry out the analysis of the facial asymmetry.
Dealing with the validation of the methods in term of accuracy, reliability and reproducibility, there is limited data. Repeatability levels in the identification of landmarks and reference lines, in the execution of the measurements and in the methods themselves, both in cephalometric and photographic tracings, appear satisfactory overall [44, 53, 56, 61, 64-66]. In terms of accuracy and reproducibility, Berlin [5] underlines in her review that “an adequate number of evenly distributed and reproducible reference points should be used, which cover all areas significant for symmetry” (she proposes 25 landmarks). “Several independent examiners should determine the reference points in order to reduce the uncertainty of subjective identification”. Using a large number of points increase both the accuracy and the expenses and using one or more reference lines can equally cause a problem if they are defined from two landmarks that are not positioned correctly. According to these considerations, the methods of Nakamura [47], Ercan [65], Baudouin [48], Trpkova [44] seem to be the most accurate as they calculate the highest number of reference points. However, they are characterized by the use of reference lines, with their associated advantages and disadvantages. In Ercan's study [65], the same investigator makes 42 landmarks twice, one month apart, and calculates the intrarater reliability coefficient for a two-facet crossed design (‘landmark pairs-by-rater-by-subject’). In Trpkova's paper [44] the investigator error is evaluated by three repeated digitizations.
The following table summarizes advantages, disadvantages and methods to quantify the asymmetry related to two-dimensional techniques (Table 3).
4.2. Three-Dimensional Techniques
Three-dimensional techniques provide more accurate and detailed information for the diagnosis and treatment planning of facial asymmetry. The disadvantages and limits that are typical of two-dimensional techniques, such as distortion, magnification and superimposition of anatomical structures are strictly reduced. However, the problem of the patient’s positioning during the examination, the need for no movements while the exam is performed (especially if clinicians use laser scanning and contact digitalization techniques) and the distortion of cephalometric measurements caused by facial asymmetry remain [67, 68].
CBCT represents the principal three-dimensional radiographic technique. It allows the exact determination and visualization of the patient’s hard and soft tissues. It makes it possible to visualize axial, sagittal and coronal sections of the acquired volume in order to obtain aorthopanoramic-like and cephalogram-like images and, through a three-dimensional rendering process, to make a three-dimensional reconstruction of the studied volume. It is significant for the identification of craniofacial disproportions and it can also be used to evaluate any causes of craniofacial asymmetries during growth, which may also arise from developmental abnormalities involving the craniofacial sutures and craniofacial modifications due to exogenous forces such as orthodontic ones [69-75]. On the other hand, CBCT exposes patients to a higher dose of radiation and it is more expensive than its two-dimensional counterparts. All authors included in this review use reference points and planes. Although the same problems exist regarding the choice of reference planes and reference points of the two-dimensional quantification of facial asymmetry, there are advantages thanks to a more accurate reconstruction of the anatomical structures and the possibility of using cranial base points as landmarks. Five authors calculate a linear asymmetry index based on the differences between bilateral distances in the three dimensions [76-80]. In particular, Katsumata [76] obtains an asymmetry index for any points that can be symmetrical, asymmetrical or marked asymmetrical. The number of landmarks used in these studies varies from 14 to 26 and the reference planes from 3 to 6, with a good balance between Yu's recommendation [50] regarding a minimum and essential number of points and measures and the need to obtain accurate measurements. Twelve authors compare bilateral distances, angles, areas and volumes for analysing facial asymmetry [12, 81-91]. Probably the easiest method used is the Hwang's one [81], which calculates six “dimensions” (starting from 12 points and 3 planes) that allow the description of the facial asymmetry comparing left and right maxillary and mandibular linear measurements and angles. Through these methods, it is possible to identify structures and “areas” mainly involved in patients’ disharmony (maxillary height, mandibular body height and length, frontal and lateral angulation of mandibular branch, mandibular branch height). It seems to be a simple method to use and to communicate to the patients. The methods of Economou and Sanders [86, 89], on the other hand, implicate the largest numbers of landmarks (38) and, consequently, the largest number of bilateral measurements.Two authors [83, 92] consider CBCT a typical modality of analysis for soft tissue disharmony: the creation of a color-coded distance map, by far the most used method to delineate the asymmetry through stereophotogrammetry [93-103]. This type of map is generated as follows. First of all, the original image of the patient's face, digitally reconstructed, is reflected around a plane that can be arbitrary external to the face itself or internal, sagittal and median. Then the two images, the original and the reflected ones, are superimposed, generally minimizing their distance through special algorithms such as ICP (Iterative Closest Point). Different colours present, in an immediate and easily understandable way, the residual distances (which represent the degrees of asymmetry) between the numerous points make up the digital images. The remaining distances can be calculated as RMSE (Root Mean Square Error), MAD (Mean Absolute Deviation) or MSD (Mean Square Distances). Eleven authors create a color-coded distance map using stereophotogrammetry [93-103], seven authors using laser scanning [42, 104-109], and two authors using 3D optical sensors [110, 111]. This type of method requires an adequate software (generally quite expensive) to superimpose images and to measure their distances but does not requires the identification of any landmarks. Two comparative studies about a landmark-based and a global or surface-based method (a method that implies the superimposition between the original image and the reflected one) have been performed by Verhoeven and Kornreich, evaluating the accuracy and the reproducibility of the methods themselves [99, 100]. Both authors claim that the “global approach” is more valid and reproducible than the landmark-based one. Moreover, intra and inter-observer performances are carefully tested by Verhoeven [93] in another paper with good results, confirmed by Kornreich [100]. The systematic error of the surface-based approach has been equally tested as well as the quality of scans or stereophotogrammetric images has been assessed [93, 95, 99, 100, 104, 105]. Given these premises, the so-called global approach, with the creation of a color-coded-distance map, seems to be the most accurate, reproducible and validated method in the literature for the quantification of soft tissue asymmetry.
There is no shortage of authors who calculate an asymmetry index or compare bilateral distances, angles and volumes [42, 89, 97, 102, 105, 106, 112-121] using stereophotogrammetry, laser scanning and 3D optical sensors. Some authors combine multiple methods. For example, Ostwald [111] calculates an asymmetry index and starting from those values, he creates a color-coded map [122]. His index allows him to easily compare the pre- and post-surgical asymmetry of the patients involved in his study. The contact digitalization techniques are rarely used (addressed in only two selected studies) [43, 123]. In particular, Sforza [43] calculates 17 unilateral and bilateral landmarks, 19 unilateral and bilateral distances between landmarks, the “individual symmetry midline” for each patient and two “gravity centres” of each side of his/her face. The deviation of landmarks from symmetry midline provides “facial midline asymmetry index”, the distance between “gravity centres” supplies “facial lateral asymmetry index” and the total of them produces “total asymmetry index”. This method is accurate and it allows a detailed analysis of the patient’s disharmony but it requires remarkable numbers of points, measurements and calculations. It also requires the patient to stay still for the time needed to complete the examination, which is not insignificant. Finally, it is necessary to remember that stereophotogrammetry, laser scanning, 3D optical sensor and contact digitalization require an adequate equipment and an initial training for their correct use [124].
The following table summarizes advantages, disadvantages and methods to quantify the asymmetry related to three-dimensional techniques (Table 4).
CONCLUSION
Clinical examination represents the first fundamental step in the diagnosis of facial asymmetry. It shows the presence of sagittal, coronal and vertical asymmetry and it is divided into an extra-oral and an intra-oral examination. Amongst 2D techniques, PA cephalogram represents the first level exam to quantify facial asymmetry, whilst an OPG can only be used to diagnose mandibular and/or condylar asymmetry. Digital photography completes the clinical evaluation and makes it more accurate. The most reliable methods to quantify facial asymmetry are those that calculate an asymmetry index based on an adequate (but not excessive) number of correctly located points, with or without the identification of reference lines. 3D techniques represent the second level examination in the diagnosis of facial asymmetry. The most used techniques are CBCT, stereophotogrammetry, laser scanning, 3D optical sensors and contact digitization. Comparing bilateral parameters (linear distances, angles, areas, volumes and contours) and calculating an asymmetry index seems to be the best choice for clinicians who use CBCT. The creation of a color-coded distance map, which is a surface-based method that requires no reference points, seems to represent the most accurate, reliable and validated method for clinicians who use stereophotogrammetry, laser scanning and 3D optical sensors.
CONSENT FOR PUBLICATION
Not applicable.
STANDARDS OF REPORTING
PRISMA guidelines and methodologies were followed in this study.
FUNDING
None.
CONFLICT OF INTEREST
The authors declare no conflict of interest, financial or otherwise.
ACKNOWLEDGEMENTS
Declared none.
SUPPLEMENTARY MATERIAL
PRISMA checklist is available as supplementary material on the publisher’s website along with the published article.


