Applications of Finite Element in Implant Dentistry and Oral Rehabilitation

All published articles of this journal are available on ScienceDirect.

REVIEW ARTICLE

Applications of Finite Element in Implant Dentistry and Oral Rehabilitation

Van V. Dam1 , 2 Hai A. Trinh1 , 2 , * Open Modal Dao T. Dung2 Trinh D. Hai2
Authors Info & Affiliations
The Open Dentistry Journal • 01 Sep 2021 • REVIEW ARTICLE • DOI: 10.2174/1874210602115010392

Abstract

Finite element is widely applied in dentistry to study the stress distributions on adjoining bone, the biomechanics of dental implant and bone; implant and bone interface and study its fatigue behaviors of the implant. This article presents various applications of finite element in implant dentistry. Available articles were searched and reviewed from March 1980 till September 2020 from Pubmed, Scopus, Google Scholar, and Science direct. Relevant studies were included and critically analyzed. Finite element is an important tool in implant dentistry to study the stress distributions on adjoining bone, the biomechanics of dental implant and bone; implant and bone interface, and fatigue behaviors.

Keywords: Dental implant, Finite element analysis, Models, Nonlinear dynamics, Biological, Stress, Mechanical.

1. INTRODUCTION

Currently, the dental implant is integrated as a routine dental treatment for the restoration of teeth, oral rehabilitation, aid in the retention, and support for the prostheses [1-3]. The dental implants present over 95% of the success rate if designed, manufactured, and inserted correctly [4]. In addition, the aid of digital technologies has enhanced the success [5]. Implants are anticipated to present their function lifelong.

Various factors influence the success of dental implants [6]. Insertion technique, surgical techniques, and clinical skills also play a vital role in the osseointegration of the dental implant. Stress of implant, jawbone, and the interactions of their biomechanical behavior establish the dental implant’s success [7].

A 3D finite element can help study the biomechanics of dental implants on the bone; stress distributions on surrounding bone, implant-bone interface, study the fatigue behaviors of implant, etc [6-9]. as shown in (Fig. 1) [8]. Various mechanical properties of important body parts and biomaterials used for the FE modeling are shown in Tables 1 and 2, respectively.

The mechanical properties of common biomaterials in implant dentistry for FE modeling are shown in Table 2. It showed a variation of Young’s modulus of elasticity and Poisson ratio among various biomaterials.

Table 1.
Mechanical properties of bone and teeth for the FE modeling.
Materials Mechanical Properties Value Study
Bone Cortical bone Young modulus, E (GPa) 13.7 [10, 11]
Poissons ratio, ʋ 0.3 [10, 11]
Cancellous bone (D1, D2, D3) Young modulus, E (GPa) 1.37 [10, 11]
Poisson ratio, ʋ 0.3 [10, 11]
Trabecular bone (D4) Young modulus, E (GPa) 1.1 [10]
Poisson ratio, ʋ 0.3 [10, 12]
Teeth Enamel Young modulus, E (GPa) 82500 [13]
Poisson’s ratio, ʋ 0.33 [13, 14]
Dentin Young modulus, E (GPa) 18600 [11, 15]
Poisson ratio, ʋ 0.31 [11, 12, 15]
Table 2.
Mechanical properties of common biomaterials in implant dentistry used for the FE modeling.
Materials Mechanical Properties Value Study
Ti Implant Abutment materials, Prosthetic Teeth Young modulus, E (GPa) 113.8 [10]
Poisson ratio, ʋ 0.34 [10]
Co-Cr Crown framework materials Young modulus, E (GPa) 218 [10]
Poisson ratio, ʋ 0.33 [10]
Porcelain Prosthetic superstructures Young modulus, E (GPa) 218 [10]
Poisson ratio, ʋ 0.35 [10]
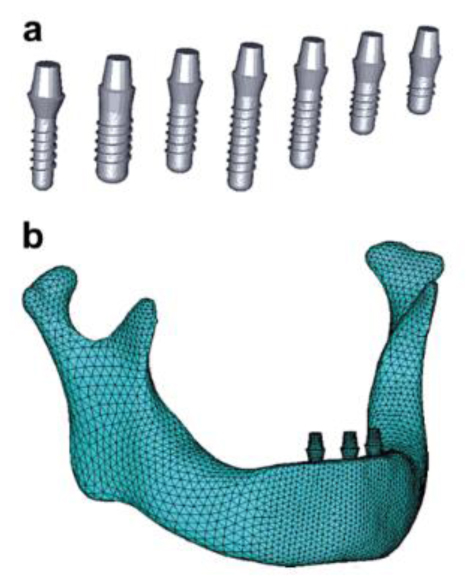
Fig. (1). Dental implants (a) and a 3D model of the mandible and dental implants with implant abutments (b) [8].

2. MECHANICAL PROPERTIES OF BONE, TEETH BIOMATERIALS FOR FINITE ELEMENT MODELING

There is a variation of Young’s modulus and Poisson ratio between enamel and dentin, and cortical, cancellous, and trabecular bone. Various mechanical properties of important body parts are shown in Table 1.

An example of finite element model is shown in Fig. (2) and it consists of the cortical, cancellous bone an implant and abutment [16]. The model is designed from a numerical strategy from the assembly of the different parts together and the stress distribution is studied.

3. APPLICATION OF FINITE ELEMENT MODELING IN IMPLANT DENTISTRY

3.1. Percentage of Osseointegration

Osseointegration of implant after placement determines the high success and survival rate of dental implants. Bone resorption and loss of the implant may be occurred because of stress around the implants. Lai et al. [17] studied the percentage of osseointegration using a FE model which was designed from the dental computed tomography. They used 3.75 x 10-mm cylindric implant in an edentulous mandible. Using a load of 35 N on the restoration at the vertical axis of the implant, the maximum principal stress, minimum principal stress, and Von Mises stress were calculated. They found that the maximum stress was distributed at the implant’s neck within the bone. The stress at the implant-tissue interface showed an inverse function to the osseointegration percentage.

3.2. Fatigue Behavior of Dental Implants

The fatigue behaviors of implant influence the stress surrounding bones. Chen et al. [18] investigated the stress at implant and interface of bone, and fatigue behaviors of Ti implant under two different loading; dynamic and static using a 3D finite element model of a mandible segment with an implant bone was constructed by CAD software. It showed that the stress present in the cortical bone was 17.15% higher under the dynamic loading than the static loading. The implant and interface at bone showed less stress than the yield strength of Ti. They concluded that the implants could transfer stress from the implant and bone interface to the bone (cancellous) and root region. The improvement in design configuration is safe under normal loading.

Fig. (2). (a) Finite element models. boundary conditions and loading (b), implant design (c), mandibular section showing various cortical thicknesses (d), configuration of the implant in the bone in the vestibulo-lingual plane (e), Von Mises stress distribution (f), a diagram of the cortical bone peri-implant area [16].

Finger amputation may result in unesthetic and function problems, which can be restored with a finger prosthesis. Amornvit et al. [19] evaluated the stress distributions around implant-retained finger prosthesis under a vertical force on the implant (4.5 mm diameter and 14 mm length) with a force of 50 N. The greatest stress was found at the abutment screw, whereas the least stress was found around the apical third. Hence, there should be a suitable biomechanical configuration to achieve the long-term success of the implant.

3.3. Sinus Lift Surgery

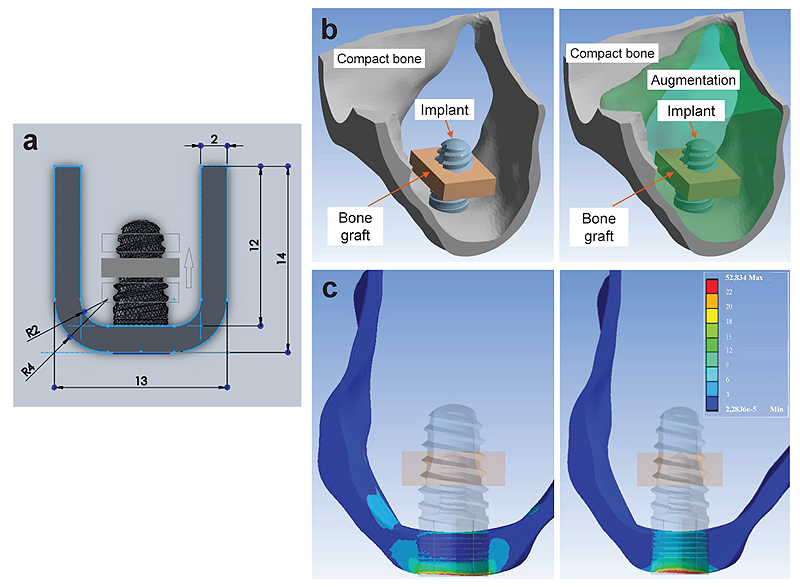
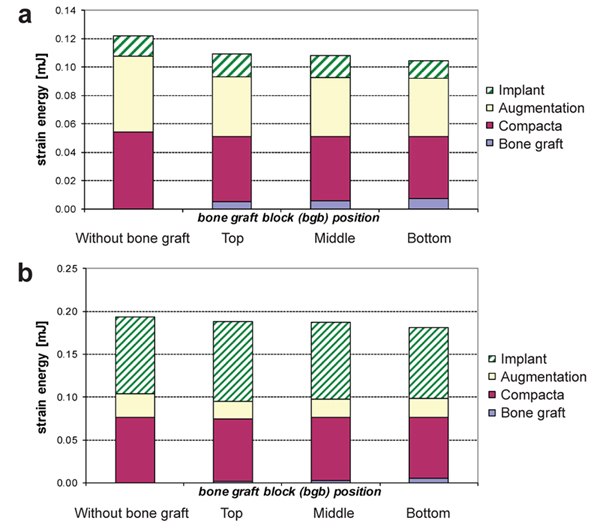
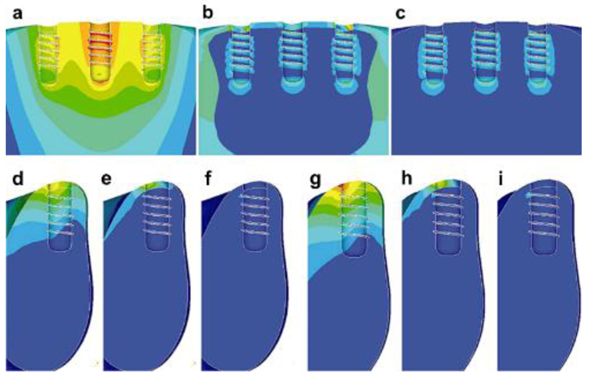
The amount and quality of the bone play a vital role in the successful rehabilitation of edentulous maxilla using implants. An inadequate bone may be caused due to various reasons resulting in bone resorption [20, 21]. Sinus lift is used commonly in bone thickness is below 2-3 mm and the patient requires bone augmentation procedures [20, 22]. Indirect sinus lift has also shown good survival rates [22-24]. Schuller-Götzburg et al. [20] evaluated sinus lift augmentation after adding block bone graft using a FE model of the maxillary molar region (Fig. 3). The stress distribution was calculated at 3 positions: at contact with the sinus floor, middle of the implant helix, and upper third of the implant. The stress for masticatory force (Fz) were 3 times lesser compared to the protrusion load (Py) (Fig. 3c). The maximum stresses occurred in the lower part of compact bone. Hence, placing the bone graft at the lower region has less strain density for the implant (Fig. 4).

4. FACTORS AFFECTING THE STRESS DISTRIBUTION AROUND IMPLANT

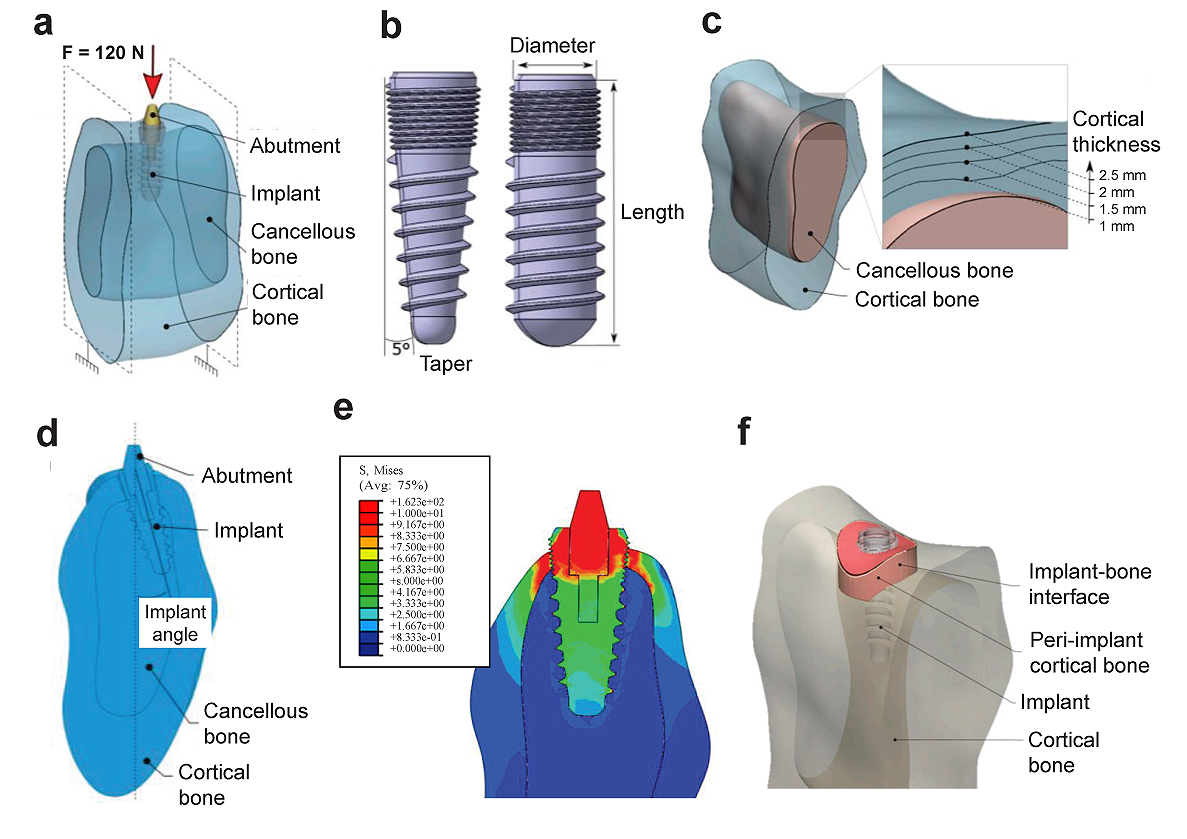
The loading on dental implants is suggested only after the adequate stability of the implant and no excessive loads should be applied. The implant diameter, length, loading angle, and insertion depth has an effect on the stress distribution [8, 25]. Didier et al. [16] investigated the several parameters (implant diameter, length, angle of inclination, taper, Young’s modulus, the thickness of the cortical bone, and Young’s modulus of the cancellous bone) on stress distribution and load transfer between the dental implant and bone using a FE model. They found that the implant diameter and Young’s modulus and the cortical thickness were the most influential parameters on the two responses.

Savadi et al. [26] studied the effect of implant surface topography and loading conditions on stress distribution using 100 (axial force) and 50 N loads (non-axial force). They found that the smooth-surfaced implant showed high punching stress at the apex of the implant. The porous-coated porous surface topography shows a more uniform distribution of stress. In another study, a surface coating of graphene oxide on the Ti implant was studied and found that they showed better mechanical behavior than graphene [27]. Recently, it has been found that graphene, graphene oxide (GO), and reduced Graphene Oxide (rGO) a potential application for coatings on titanium alloys [28-31]. More clinical trials are required to validate the findings of the present study [27].

Fiorillo et al. [32] found that the results on this new type of connection and on all the implant components are satisfactory; the distribution of forces (800 N) was optimal on the peri-implant tissues. Ding et al. [8] studied the role of the implant length and implant diameter on the stress distribution in the mandible around dental implants design after using a FE model from CT using a load of 150 N (Fig. 5). They used seven Straumann implant design of implant length (6 - 14 mm) and implant diameter (3.3 - 4.8 mm). It showed that the oblique force compared to the vertical force resulted in excessive stresses and strains on the implant and the bone. Hence, increasing the diameter and length of the implant decreases the stress and strain on the bone. The diameter affects more to relieve the stress and strain compared to the length. Similarly, Ding et al. [33] also mentioned that an increasing implant diameter significantly decreases the stress and strain on the implant and bone interfaces where they experimented in three mandible models. It also showed that the implants with a length of 10 mm should be at least 4.1 mm in diameter to result in less stress on the bone. In addition, oblique forces to implants must be minimized or avoided.

Fig. (3). (a) Finite element model with the block bone graft showing the various positions of the block bone graft (b), U-shaped compact bone model, the implant, and the bone graft in middle (left) and compact bone with augmentation (right) (c), Stress in bone with the bone graft placed in the center [20].
Fig. (4). (a) Results of the finite element model with the block bone graft at the center of the implant (b), Anatomical model of the maxilla and the bone graft in middle (c), and compact bone with augmentation [20].

Another study investigated the role of dental implant diameter, loading angle, and insertion depth on stress and strain in a jawbone using the FE study [25]. Application of the maximum load of 200 N in various loading angles (0 to 85 degrees) buccolingually, they found that the maximum stress was at the cortical bone on the lingual side adjacent to the implant. Larger diameter implant and increased insertion depth substantially improved the stress/strain distribution. Implant loaded at an oblique loading angle in a shallow insertion depth is most harmful to bone and implant. Hence, an enhanced implant neck design and an adequate depth implant are favorable for the bone in implant/bone systems.

Fig. (5). (a-c) Fields distribution with implant diameter and length (4.1 x 10 mm) under vertical loading and oblique loading (d-i) using finite element study [8].

De Moraes et al. [34] studied the diameter, implant loading, and type of the connection on stress patterns in the bone with an increased crown-implant ratio. They applied an axial force (200 N) or oblique force (100 N) on the dental implant with 8.5 mm length, diameter 3.75 or 5 mm, and various connection types; internal hexagon external hexagon, and Morse taper using posterior mandibular region 3D models with the InVesalius, Rhinoceros 3D 4.0 and SolidWorks 2011 software programs. Models were processed using the Femap 11.2 and NeiNastran 11.0 programs. It was found that the angled compared to axial loading showed high stress in the cortical bone. They found that with the application of oblique force, the stress was high in the cortical bone compared to the axial force. Wider diameter implants showed favorable stress distribution irrespective of the type of connection. In addition, Morse taper implants presented the favorable distribution of the stress, especially in the oblique loading.

The short implants may be considered if sufficient bone height is not present mandibular arch [35-37]. Vidya Bhat et al. [35] evaluated the influence of implant lengths (6, 8, 10, and 13 mm) on stress in the mandibular arch using a FE model by applying a static vertical force (250 N) and a horizontal force (100 N). The baseline demographic variables, including age, gender and smoking status, bone quality, location, implant dimensions, and types of prostheses, were compared to ensure balance among groups. They found that under the vertical load, the short implants were able to tolerate loads and disseminate reduced load to the bone. Bruxing forces must be minimized by increasing the number and diameter of the implants [37].

5. LIMITATIONS OF FE STUDIES IN IMPLANT DENTISTRY

Although the FE method is a precise method for analyzing structures, they have certain limitations [19, 35, 38]:

  • The implant and bone interface is predicted as a continuous bond.
  • No micro-movement at the implant and bone interface during loading which is different from the real clinical situation.
  • Osseointegration is expected 100%, which is ideal and never true in the clinical situation.
  • The bone (cortical, cancellous) and implant are taken as isotropic and homogenous but in real the bone is anisotropic and inhomogeneous.
  • The implant is rigidly anchored in the bone.
  • The loads were applied only at point locations.
  • The force applied duration in the implants and oral cavity differs.

Furthermore, in most FE studies, generally, only a single loading point and angle are tested rather than an episode of stress as in clinical situation [39]. Hence the FE studies lack the fatigue, aging, thermal, and continuous mechanical cyclic loading when analyzing the prosthetic dental implant. In many finite element studies, they use optimal force. Further studies should be done considering all these factors.

CONCLUSION

Finite element is an important tool in implant dentistry to study the stress distributions on adjoining bone, the biomechanics of dental implant and bone; implant and bone interface and study the fatigue behaviors of the implant. It has been shown that a wide diameter and longer implant provide suitable stress distribution in the bone. Morse taper implants show less stress. Future innovations would be creating a micro-movement at the implant and bone interface during loading to simulate the real clinical situation.

CONSENT FOR PUBLICATION

Not applicable.

FUNDING

None.

CONFLICT OF INTEREST

The authors declare no conflict of interest, financial or otherwise.

ACKNOWLEDGEMENTS

Declared none.

REFERENCES

1
Setzer FC, Kim S. Comparison of long-term survival of implants and endodontically treated teeth. J Dent Res 2014; 93(1): 19-26.
2
Amornvit P, Bajracharya S, Rokaya D, Keawcharoen K, Supavanich W. Management of obstructive sleep apnea with implant retained mandibular advancement device. World J Dent 2014; 5(3): 184-9.
3
Rokaya D, Srimaneepong V, Wisitrasameewon W, Humagain M, Thunyakitpisal P. Peri-implantitis update: Risk indicators, diagnosis, and treatment. Eur J Dent 2020; 14(4): 672-82.
4
Romeo E, Lops D, Margutti E, Ghisolfi M, Chiapasco M, Vogel G. Long-term survival and success of oral implants in the treatment of full and partial arches: A 7-year prospective study with the ITI dental implant system. Int J Oral Maxillofac Implants 2004; 19(2): 247-59.
5
Humagain M, Rokaya D. Integrating digital technologies in dentistry to enhance the clinical success. Kathmandu Univ Med J (KUMJ) 2019; 17(68): 256-7. [KUMJ].
6
Amornvit P, Rokaya D, Keawcharoen K, Raucharernporn S, Thongpulsawasdi N. One- vs two stage surgery technique for implant placement in finger prosthesis. J Clin Diagn Res 2013; 7(9): 1956-68.
7
Van Staden RC, Guan H, Loo YC. Application of the finite element method in dental implant research. Comput Methods Biomech Biomed Engin 2006; 9(4): 257-70.
8
Ding X, Liao SH, Zhu XH, Zhang XH, Zhang L. Effect of diameter and length on stress distribution of the alveolar crest around immediate loading implants. Clin Implant Dent Relat Res 2009; 11(4): 279-87.
9
Paracchini L, Barbieri C, Redaelli M, Di Croce D, Vincenzi C, Guarnieri R. Finite element analysis of a new dental implant design optimized for the desirable stress distribution in the surrounding bone region. Prosthesis 2020; 2: 225-36.
10
Yalçın M, Kaya B, Laçin N, Arı E. Three-dimensional finite element analysis of the effect of endosteal implants with different macro designs on stress distribution in different bone qualities. Int J Oral Maxillofac Implants 2019; 34(3): e43-50.
11
Menicucci G, Mossolov A, Mozzati M, Lorenzetti M, Preti G. Tooth-implant connection: Some biomechanical aspects based on finite element analyses. Clin Oral Implants Res 2002; 13(3): 334-41.
12
MacGregor AR, Miller TP, Farah JW. Stress analysis of mandibular partial dentures with bounded and free-end saddles. J Dent 1980; 8(1): 27-34.
13
Farah JW, Craig RG, Meroueh KA. Finite element analysis of three- and four-unit bridges. J Oral Rehabil 1989; 16(6): 603-11.
14
Farah JW, Hood JA, Craig RG. Stresses and deflections in the floor of model cavity preparations. J Oral Rehabil 1974; 1(2): 207-15.
15
Reinhardt RA, Pao YC, Krejci RF. Periodontal ligament stresses in the initiation of occlusal traumatism. J Periodontal Res 1984; 19(3): 238-46.
16
Didier P, Piotrowski B, Le Coz G, Joseph D, Bravetti P, Laheurte P. Finite Element Analysis of the Stress Field in Peri-Implant Bone: A Parametric Study of Influencing Parameters and Their Interactions for Multi-Objective Optimization. Appl Sci (Basel) 2020; 10: 5973.
17
Lai H, Zhang F, Zhang B, Yang C, Xue M. Influence of percentage of osseointegration on stress distribution around dental implants. Chin J Dent Res 1998; 1(3): 7-11.
18
Chen L, Guo X, Li Y, Li T. Finite element analysis for interfacial stress and fatigue behaviors of biomimetic titanium implant under static and dynamic loading conditions. Zhong Nan Da Xue Xue Bao Yi Xue Ban 2010; 35(7): 662-72.
19
Amornvit P, Rokaya D, Keawcharoen K, Thongpulsawasdi N. Stress distribution in implant retained finger prosthesis: A finite element study. J Clin Diagn Res 2013; 7(12): 2851-4.
20
Schuller-Götzburg P, Id T. Forte, Pomwenger W, Petutschnigg A, Watzinger F, Entacher K. Three-dimensional finite element analysis of maxillary sinus floor augmentation with optimal positioning of a bone graft block. Symmetry (Basel) 2018; 10(2): 33.
21
Trinh HA, Dam VV, Banlunara W, Sangvanich P, Thunyakitpisal P. Acemannan induced bone regeneration in lateral sinus augmentation based on cone beam computed tomographic and histopathological evaluation. Case Rep Dent 2020; 2020: 1675653-3.
22
Trinh HA, Dam VV, Le B, Pittayapat P, Thunyakitpisal P. Indirect sinus augmentation with and without the addition of a biomaterial: a randomized controlled clinical trial. Implant Dent 2019; 28(6): 571-7.
23
Shi J-Y, Gu Y-X, Zhuang L-F, Lai H-C. Survival of implants using the osteotome technique with or without grafting in the posterior maxilla: A systematic review. Int J Oral Maxillofac Implants 2016; 31(5): 1077-88.
24
Srouji S, Kizhner T, Ben David D, Riminucci M, Bianco P, Livne E. The Schneiderian membrane contains osteoprogenitor cells: In vivo and in vitro study. Calcif Tissue Int 2009; 84(2): 138-45.
25
Qian L, Todo M, Matsushita Y, Koyano K. Effects of implant diameter, insertion depth, and loading angle on stress/strain fields in implant/jawbone systems: Finite element analysis. Int J Oral Maxillofac Implants 2009; 24(5): 877-86.
26
Savadi RC, Agarwal J, Agarwal RS, Rangarajan V. Influence of implant surface topography and loading condition on stress distribution in bone around implants: A comparative 3D FEA. J Indian Prosthodont Soc 2011; 11(4): 221-31.
27
Patil V, Naik N, Gadicherla S, Smriti K, Raju A, Rathee U. Biomechanical behavior of bioactive material in dental implant: A three-dimensional finite element analysis. ScientificWorldJournal 2020; 20202363298
28
Srimaneepong V, Rokaya D, Thunyakitpisal P, Qin J, Saengkiettiyut K. Corrosion resistance of graphene oxide/silver coatings on Ni-Ti alloy and expression of IL-6 and IL-8 in human oral fibroblasts. Sci Rep 2020; 10(1): 3247.
29
Rokaya D, Srimaneepong V, Qin J, Siraleartmukul K, Siriwongrungson V. Graphene oxide/silver nanoparticle coating produced by electrophoretic deposition improved the mechanical and tribological properties of NiTi alloy for biomedical applications. J Nanosci Nanotechnol 2019; 19(7): 3804-10.
30
Podila R, Moore T, Alexis F, Rao A. Graphene coatings for biomedical implants. J Vis Exp 2013; (73): e50276-6.
31
Rokaya D, Srimaneepong V, Thunyakitpisal P, Qin J, Rosa V, Sapkota J. Potential applications of graphene-based nanomaterials in biomedical, dental, and implant applications.Advances in Dental Implantology using Nanomaterials and Allied Technology Applications 2021; 77-105.
32
Fiorillo L, Cicciù M, D’Amico C, Mauceri R, Oteri G, Cervino G. Finite element method and von mises investigation on bone response to dynamic stress with a novel conical dental implant connection. BioMed Res Int 2020; 20202976067
33
Ding X, Zhu X-H, Liao S-H, Zhang X-H, Chen H. Implant-bone interface stress distribution in immediately loaded implants of different diameters: A three-dimensional finite element analysis. J Prosthodont 2009; 18(5): 393-402.
34
Moraes SLD, Verri FR, Santiago JFJ, et al. Three-dimensional finite element analysis of varying diameter and connection type in implants with high crown-implant ratio. Braz Dent J 2018; 29(1): 36-42.
35
Vidya Bhat S, Premkumar P, Kamalakanth Shenoy K. Stress distribution around single short dental implants: A finite element study. J Indian Prosthodont Soc 2014; 14(Suppl. 1): 161-7.
36
Feldman S, Boitel N, Weng D, Kohles SS, Stach RM. Five-year survival distributions of short-length (10 mm or less) machined-surfaced and Osseotite implants. Clin Implant Dent Relat Res 2004; 6(1): 16-23.
37
Lum LB. A biomechanical rationale for the use of short implants. J Oral Implantol 1991; 17(2): 126-31.
38
Savadi RC, Agarwal J, Agarwal RS, Rangarajan V. Influence of implant surface topography and loading condition on stress distribution in bone around implants: A comparative 3D FEA. J Indian Prosthodont Soc 2011; 11(4): 221-31.
39
Guragain M, Mathema S, Rokaya D. Evaluation of fracture resistance and sites of failure of different dowel core restorations: An in-Vitro study. Open Dent J 2019; 13: 454-61.